TASKIN HARPSICHORD SCALINGS AND STRINGINGS REVISITED
Part 3 - Appendixes and Bibliography
Copyright © 2011 by Claudio Di Veroli, Bray Baroque, Bray, Ireland, March 2011

Contents
Back
Back to Part 1
Back to Part 2
Appendix 1 - Improving Wraight's Nuremberg Synthesis
Appendix 2 - Hypothetical reconstruction of the Taskin 1769 original schedule
Literature Cited
Appendix 1 - Improving Wraight's Nuremberg Synthesis
Denzil Wraight's comprehensive paper (Wraight 2000) is compulsory reading for anybody interested in the reconstruction of 18th century keyboard string gauges. Ancient data are very scarce and slightly diverse, because wires were not absolutely uniform. Even worse, no 18th-century data is extant for gauges 00, 9 and 10. To resolve these serious uncertainties, Dr. Wraight carried out an in-depth study of the wire-drawing process and postulated that, for most of the gauges in use for harpsichords (numbers 1 to 12) their diameters strictly followed a geometrical sequence with ratio 19/17. For larger gauges (0, 00, 000 and so on) he extrapolated with different numbers of "steps". Wraight named his final set of wire sizes "Nuremberg synthesis" (Wraight op.cit. p.212): it produces an overall approximation model to extant data for both harpsichords and early pianos. The approximation is quite good if we consider the above-mentioned scarcity of data.
Unfortunately, if one is particularly interested in 18th harpsichords, the Nuremberg synthesis, however plausible, is not the best possible fit to the available data (Wraight acknowledges this on p. 185). From a statistical point of view, the author finds it better in this case to give more weight to the individual data rather than to a hypothetical progression. The final changes shown below with respect to Wraight may look minor, and so they are in 8 of the 15 gauges, but in the others they are significant. In some gauges Wraight's sizes are smaller, in others they are larger, implying an increase in tensions between 2.3 % and quite significant 4.9 %. Finally, in gauge 11 the increase is 8.7 %: here the Nuremberg synthesis model produces a diameter of 0.172mm (.0068"), but the only 18th c. extant evidence is a wire measuring 0.168mm and, by interpolation with adjacent gauges, one gets an even smaller size, 0.165mm (.0065"). These considerations show, in the opinion of the present author, the advantage—for this particular problem and data set—of leaving aside a general hypothetical mathematical model, and producing instead individual estimates for each gauge number, using mainly the available data: local interpolation or regression are also used, but limited to a few consecutive gauges and only when strictly needed.
The data used here are taken from Wraight's very well documented paper, although some data have also been considered that he did not enter in his main Table 4. The arguments below are to be read as minor improvements on Wraight's system, and for this reason this Appendix has been written as a self-contained text, trying however to avoid repeating information and bibliography already included in Wraight's work. The estimates below begin from gauge 6, for which we have some good 18th c. evidence. Lüdicke's data—with the longest gauge sequence from the harpsichord era—is used as a backbone to be improved by comparison with other data.
Interestingly, a simple logarithmic regression fits Lüdicke's gauges 8 to 4 relatively well, but they fail the sequence in gauge 6, where Lüdicke has 0.302 but the logarithmic regression suggests 0.304, and Wraight's model is 0.306. Further, these numbers go straight against Cryseul's single value of 0.297. This and other features of the data show that fixing the paucity of data by means of an overall mathematical model may be misleading, and that a better estimate is likely to be reached by applying statistical judgements to individual gauges or partial sequences.
In the list below we do not include the lengthy individual calculations: we only abridge the main conclusions and also comment on the approximation with modern wire gauges. The numbers in bold type below are to be read as follows:
Gauge number - Wraight Nuremberg Synthesis(mm) - new suggested value in mm - same in inches - rounded to modern sizes
GAUGE 6 - 0.301 - 0.300 - .0118" - .012". Tiella's measurement of extant wire with 0.307 is obviously too high. Lüdicke's .298 is too low compared with logarithmic regressions of his own other gauges. Thus Cryseul's .297 was surely a sample lower than average. Wraight's table gives the very plausible 0.301. All things considered and weighted, our new estimate is 0.300, only by coincidence a rounded value.
GAUGE 5 - 0.336 - 0.339 - .0133" - .013". Tiella is also high here at 0.342 (not to mention the late and dubious Hachette's 0.345). Lüdicke's 0.338 is slightly low and a logarithmic smoothing of his data yields here 0.339. This looks like a good estimate, and there seems to be no reason for going as low as Wraight's 0.336. Note that the equivalent of 0.339 mm is .0133", poorly approximated by modern .013".
GAUGE 4 - 0.375 - 0.377 - .0148" - .014" (or .015"). As a rule, Hachette's sizes have been disregarded here, as they date from 1824 and are mostly larger than 18th century values: he has here 0.386. Tiella's 0.371 suggests that Lüdicke's 0.379 may also be on the high side. Logarithmic regression in Lüdicke yields 0.378 and Wraight's synthesis 0.375. All things weighted, our new estimate is 0.377. Its equivalent .0148" is badly approximated by modern .014": a yellow brass in .015" (still uncommon nowadays) is really useful here.
GAUGE 3 - 0.420 - 0.410 - .0161" - .016". Lüdicke here has 0.406. This is—as already noted by Wraight—very small and much outside any geometric sequence with his data: therefore, neither the logarithmic regression best fit of 0.421 nor the virtually identical 0.420 by Wraight are much significance here. Lüdicke obviously needs amending up, but not to the point of significantly bending data simply to follow a mathematical model that does not fit anyway. Lacking better information, the author prefers to practice only a modest correction to Lüdicke, bringing the estimate up to 0.410.
GAUGE 2 - 0.469 - 0.463 - .0182" - .018". Here we only have Lüdicke and Thomée, both at 0.460. Wraight coincides with a logarithmic regression of Lüdicke: both are 0.469 (.0185"). Nevertheless, these poorly fitting curves should not be taken at face value: they are only good in pinpointing the direction of the error. All things considered, the author prefers a more limited amendment up from 0.460, reaching only 0.463.
GAUGE 1 - 0.524 - 0.518 - .0204" - .020". We agree that Lüdicke is too low at 0.501: log regression is 0.523, early pianos 0.515, Coulomb weighted-ave. 0.520. The very late Thomée is 0.510 which, corrected by his tendency of being about 0.007 too low in this gauge range, can be corrected up to about 0.517. Everything seems to point to an unknown value in the range from 0.515 to 0.520. All things considered, our new estimate is 0.518.
GAUGE 0 - 0.577 - 0.572 - .0225" - .022". Lüdicke's is again a bit low at 0.568. Conversely a logarithmic regression of his data is here 0.584, surely too high. Thomée is 0.560, which as before is corrected as 0.567. More significantly, early pianos average 0.575. All things weighted, a reasonable estimate is 0.572.
GAUGE 00 - 0.629 - 0.620 - .0244" - .024". No Lüdicke value is available. The .0620 of early pianos (Wraight p.204) is the best estimate. It is virtually identical to Wraight's steps model: 6 wire-drawing steps up from Gauge 1, assumed 0.524, yield 0.619. [For reasons not clear from his paper, Wraight in the "Nuremberg Synthesis" column of his Table 4 instead of 0.619 has 0.629: a typo perhaps?]
GAUGE 000- 0.689 - 0.685 - .0269" - .027". Tiella's old wire is 0.690, but early pianos have 0.675. A reasonable estimate is 0.685, very near to Wraight's synthesis. Incidentally, none of the French sources listed above in this study study uses this gauge: the only French source known to the author that includes it is the Encyclopédie. Let us now go back and calculate gauges 7-12.
GAUGE 7 - 0.269 - 0.269 - .0106" - .011". Lüdicke's 0.271 fits his own data better than Tiella's .270: the Lüdicke logarithmic regression yields 0.272. On the other extreme, Coulomb's iron/brass average is 0.265. This again seems to show that Lüdicke's wires did not strictly follow a geometric progression. The new estimate here agrees with Wraight's synthesis: 0.269 or .0106". This is poorly approximated by modern .011".
GAUGE 8 - 0.241 - 0.244 - .0096" - .010". The only ancient data here is Lüdicke 0.244, which is consistent with a progression from his other data: thus it seems sensible to follow Lüdicke here rather than Wraight's model. The equivalent 0096" is, again, poorly approximated by modern .010". There is no ancient data available for Gauges 9 and 10, which need to be extrapolated: therefore, let us deal first with GAUGE 11.
GAUGE 11 - 0.172 - 0.165 - .0065" - .007". Here we only have Tiella's 0.168 and the late Hachette's 0.160. There is no apparent reason for going as high as Wraight's 0.172, just for the sake of a general geometrical progression. A value of 0.165 seems far more reasonable. The only equivalent available nowadays is .007" in steel. Anyway this gauge is never found in Baroque French harpsichords: Corrette (1753 p.81) observed that this wire was good only to make wigs. Therefore, this value is not needed for real-life harpsichord stringing: it is used here only to allow interpolating for GAUGES 9 and 10, for which no ancient data is extant.
GAUGE 12 - 0.154 - 0.153 - .0060" - .006". Here we have Tiella 0.155 and Coulomb 0.150. A good ave. is 0.153. This "wig gauge" is also never found in Baroque French harpsichords: we have estimated it here only to help in interpolating for GAUGES 9 and 10.
GAUGE 9 - 0.215 - 0.214 - .0084" - .008". As said above, we have no historical data here and we need to interpolate. This is not difficult to do: there are two methods and we have calculated both. One is Geometrical Interpolation (GI) between gauges 8 and 11; the other is Logarithmic Regression (LR) involving gauges 7 to 12. For Gauge 9 GI yields 0.2142, while LR yields 0.2140; thus the latter value can be taken as a representative of both methods. Its equivalent in inches is poorly served by modern wire sizes.
GAUGE 10 - 0.193 - 0.189 - .0074" - .007". Here Geometrical Interpolation yields 0.1880 and Logarithmic Regression 0.1902. The average is 0.1891, equivalent to 0.0074", which is best approximated by modern 0.007" and of use only in the extreme treble of the 4'. With standard modern iron wire, we have to use either iron 0.008" or safer steel 0.007". [Note how GAUGE 11 was approximated by the same modern size 0.007": luckily this is not a practical issue, because GAUGE 11 is never used in French harpsichords.]
Note also how GAUGE 8 above is 0.0096", best approximated by modern .010", while GAUGE 9 is 0.0084" thus best using modern .008" (the same problem is observed if one uses Wraight's synthesis). We have thus two ancient gauges that differ by 0.0012" while their modern counterparts differ by 0.0020". Therefore, if we copy an instrument and blindly use its ancient schedule approximated with modern wire, we introduce a significant gap in pulls: a detailed analysis of the instrument's pull curve is needed in order to produce, using modern wire, a stringing schedule that follows ancient pulls accurately.
As a conclusion, it is relevant to stress once again that Denzil Wraight's well-researched paper was instrumental in laying the basis for further study, including this one. This said, for French harpsichords the author finds it safe and preferable to use the slightly amended values explained above. Needless to say, both Wraight's mathematical model and the author's data analysis are approximations to values that historically were not very consistent either: the accuracy will be further improved when in the future, hopefully, further ancient wire, markings or documents are found and investigated. Finally, please note that the lack of good equivalences with modern wire is not a serious problem in practice because, as said above, a stringing schedule has to be calculated using modern available sizes. Lately some string makers are introducing additional modern gauges, yielding better approximation to historical ones. Summarizing, when we calculate pulls we should use ancient wire sizes for the analysis of ancient instruments, and available modern wire sizes instead for present-day stringing practice.
Please find below a table with all the data we have used above.
Table 7 - Sources for French 18th
and 19th c. string gauges (Wraight 2000) and the author’s proposal
|
Gauge |
Old
wire |
Lüdicke |
Cryseul |
Coulomb |
Pianos |
Hachette |
Thomée |
|
Di Veroli |
Tension |
Di Veroli |
|
|
|
1781 |
1780 |
1784 |
1790-1818 |
1824 |
1866 |
Synthesis |
2011 |
diff. |
2011 |
|
|
1764 |
|
|
ave. |
ave. |
|
|
Wraight p.212 |
|
Wraight
vs Di V. |
|
|
Nº |
mm |
mm |
mm |
mm |
mm |
mm |
mm |
mm |
mm |
% |
in |
|
000 |
0.690 |
|
|
|
0.675 |
|
0.66 |
0.689 |
0.685 |
1.2 % |
.0270 |
|
00 |
|
|
|
|
0.617 |
|
0.60 |
0.629 |
0.620 |
2.9 % |
.0244 |
|
0 |
|
0.568 |
|
|
0.575 |
|
0.56 |
0.577 |
0.572 |
1.8 % |
.0225 |
|
1 |
|
0.501 |
|
0.515 |
0.515 |
|
0.51 |
0.524 |
0.518 |
2.3 % |
.0204 |
|
2 |
|
0.46 |
|
|
|
|
0.46 |
0.469 |
0.463 |
2.6 % |
.0182 |
|
3 |
|
0.406 |
|
|
|
|
0.41 |
0.420 |
0.410 |
4.9 % |
.0161 |
|
4 |
0.371 |
0.379 |
|
|
|
0.386 |
0.37 |
0.375 |
0.377 |
-1.1 % |
.0148 |
|
5 |
0.342 |
0.338 |
|
|
|
0.345 |
0.32 |
0.336 |
0.339 |
-1.8 % |
.0133 |
|
6 |
0.307 |
0.302 |
0.297 |
|
|
|
0.28 |
0.301 |
0.300 |
0.7 % |
.0118 |
|
7 |
0.270 |
0.271 |
|
0.265 |
|
|
0.25 |
0.269 |
0.269 |
0.0 % |
.0106 |
|
8 |
|
0.244 |
|
|
|
|
|
0.241 |
0.244 |
-2.4 % |
.0096 |
|
9 |
|
|
|
|
|
|
|
0.215 |
0.214 |
0.9 % |
.0084 |
|
10 |
|
|
|
|
|
|
|
0.193 |
0.189 |
4.3 % |
.0074 |
|
11 |
0.168 |
|
|
|
|
0.16 |
|
0.172 |
0.165 |
8.7 % |
.0065 |
|
12 |
0.155 |
|
|
0.150 |
|
|
|
0.154 |
0.153 |
1.3 % |
.0060 |
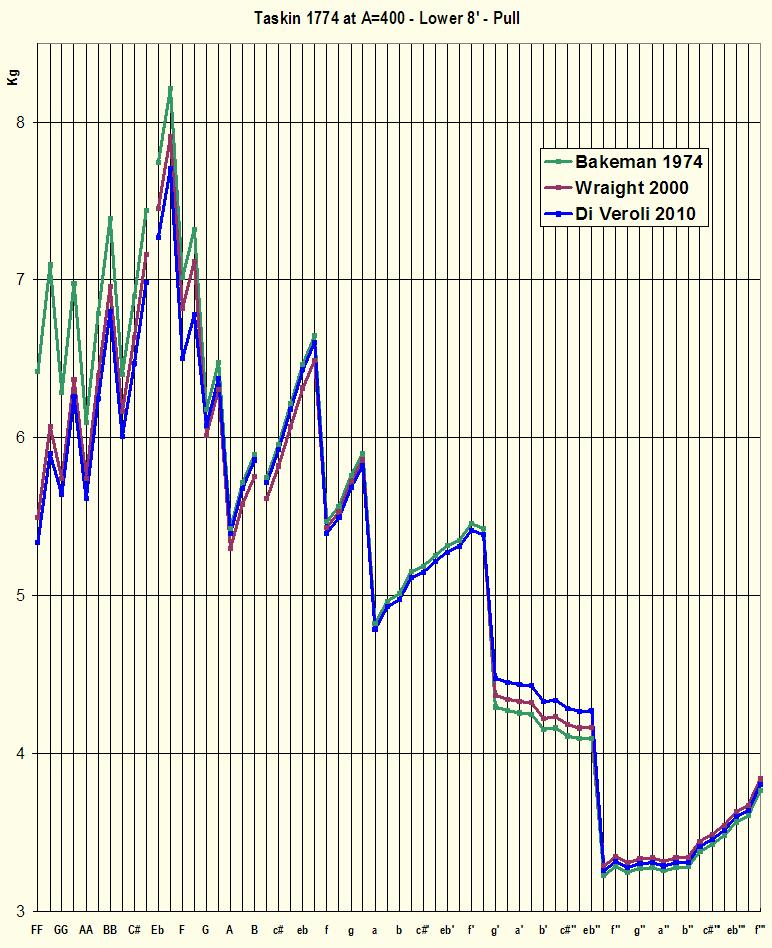
Fig. 6 - The pull produced by the original schedule in the Brussels Taskin
1774,
with three different hypotheses about the meaning of the ancient gauge numbers
T
Appendix 2 - Hypothetical reconstruction of the Taskin 1769 original schedule
The Taskin 1769 in Edinburgh is important as the model for a high percentage of the double French harpsichords built in modern times. Therefore, for any historical analysis of stringing, it is highly desirable to use its scaling and schedule. Unfortunately, no schedule data is extant for this instrument. The Edinburgh museum's schedule (O'Brien 2000) was based on a now obsolete wire gauge conversion, and was largely derived by comparison with the other Taskin in the Edinburgh collection, for which the schedule is extant instead, the Goermans-Taskin. Unfortunately, the latter—as we have seen above in this study—has a very different and non-Taskin bridge shape in the bass, with a much larger scaling, surely meant for a significantly lower pitch. The Edinburgh schedule for the Taskin 1769 produces, in the author's opinion, a stringing that is too light for the 8' choirs at the presumed original pitch A=400 Hz. Conversely, with the instrument's present A=415 Hz pitch, the stringing is too heavy for the 4' choir. These problems will be apparent further below.
With the present better understanding of string gauges, and with more instruments available for comparison, the author has preferred to deduce the schedule for the Taskin 1769 using as a starting point the almost contemporary Taskin 1774 (today in the Brussels Museum) which has the schedule inscribed in the wrestplank. The scaling is still larger than the 1769 in the bass, but significantly less so than the Goermans-Taskin. Even more importantly, our comparison of scalings, schedules and pulls concluded that the pitches of the 1769 and 1774 instruments are very likely to have been identical. Even if the extant 1769 instrument is at present tuned at A=415 Hz, most writers agree that the original pitch was midway between old A=392 Hz and Taskin's extant tuning fork of 1784 at A=409 Hz, i.e. around A=400 Hz. Remarkably, we have seen in Section 6 that this pitch provides the best match for its pulls compared with other Taskin instruments.
The schedule deduction process begins by simply applying the 1774 schedule to the 1769 instrument. Having computed the pulls for each string, we proceed to amend the few strings where the pulls fall outside the pull ranges and pull-curve features seen in other instruments by Taskin, as scrutinised in the main body of this study. Given the many constraints, the possible variations are scarcely significant. Find in Table 8 below the final reconstructed schedule: for each range, the alloy is followed by the French gauge number and the conversion to wire sizes in inches, following our gauge conversion system shown in Appendix 1.
Table 8 - Reconstructed Stringing Schedule for the Taskin 1769, now in Edinburgh, at A=400 Hz
(Alloys: RB=Red Brass, YB=Yellow Brass, IR=Iron)
8' 4'
e" - f'" IR 9 .0084" g#"- f'" IR 10 .0074"
f' - eb" IR 8 .0096" c#"- g" IR 9 .0084"
a - e' IR 7 .0106" g# - c" IR 8 .0096"
e - g# IR 6 .0118"
c - eb IR 5 .0133" d - g IR 7 .0106"
Bb - B YB 5 .0133" Bb - c# IR 6 .0118"
G# - A YB 4 .0148" G - A YB 6 .0118"
F - G YB 3 .0161"
Eb - E YB 2 .0182" F - F# YB 5 .0133"
C# - D RB 2 .0182" Eb - E YB 4 .0148"
BBb - C RB 1 .0204" C - D RB 4 .0148"
GG# - AA RB 0 .0225" GG# - BB RB 3 .0161"
FF - GG RB 00 .0244" FF - GG RB 2 .0182"
The figures below show the pull curves. [Note: in spreadsheets, "later curves", i.e. lower in the list, overwrite the others when they coincide].
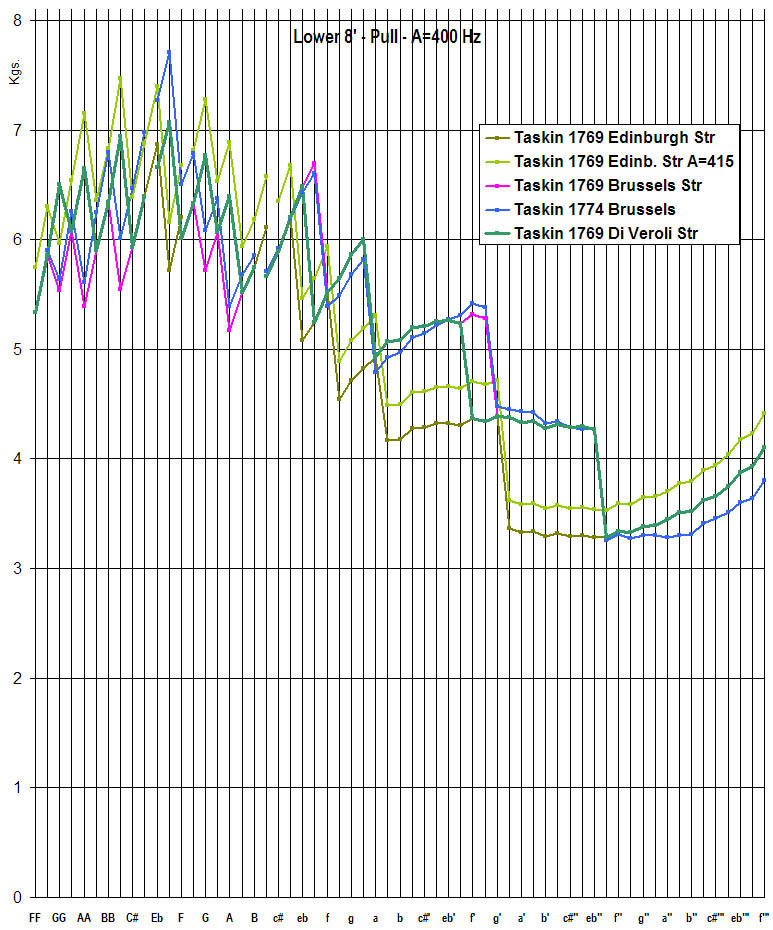
Fig. 8 - Different hypothetical schedules for the Taskin 1769 harpsichord: lower 8' choir
In the above chart the problems with the present Edinburgh 8' schedule are apparent:
- In the Red Brass the stringing is slightly too heavy for the present A=415 Hz: also, the transition to Yellow Brass is two semitones higher than in any historical schedule.
- The Yellow Brass is slightly too light for A=400, but again too heavy for A=415.
- In the two midrange octaves eb-eb" the stringing is too light for either A=400 or 415.
Fig. 8 shows how all the above issues are resolved in our proposed new schedule for A=400 Hz.
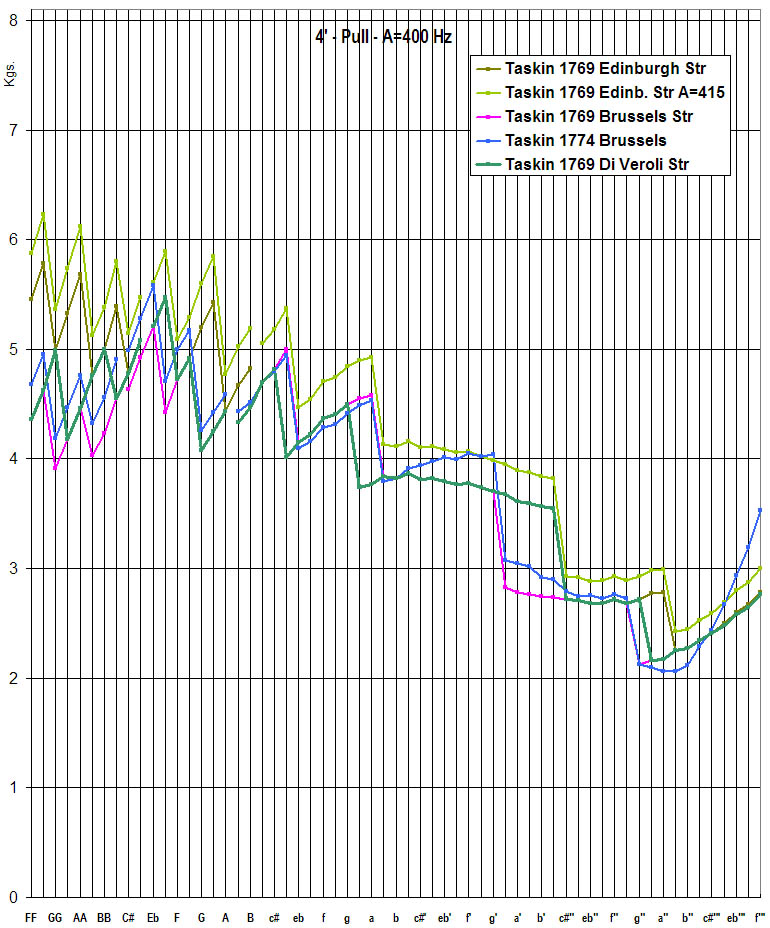
Fig. 9 - Different hypothetical schedules for the Taskin 1769 harpsichord: 4' choir
[Note: in the range c-f#", the "Edinburgh Str" curve is overwritten by the identical "Di Veroli Str" curve]
The chart above shows that the Edinburgh 4' schedule is too heavy for the Red Brass. It is fine for the rest of the range, but not if the instrument is tuned to A=415 Hz. Again, all the issues are resolved in the new reconstructed schedule for A=400 Hz.
To conclude, this Appendix shows that, without any pretence at absolute accuracy, the new reconstructed schedule fits available historical data significantly better than the Museum's schedule, even if the latter is interpreted as fitting the present A=415 Hz pitch. The new schedule detailed above looks robust enough to be added to the other scaling-schedule pairs used in this article in order to derive common traits for Taskin's harpsichords.
Note: The reconstructed 8' and 4' schedules shown above are meant to be used for historical comparisons and also, quite obviously, for stringing the instrument at the historically-likely A=400 Hz, with the few changes needed to allow for modern wire sizes. Needless to say, for the present pitch of this instrument in Edinburgh at A=415, a different schedule should be calculated, whereby some strings need a smaller size to avoid excessive pulls.
This is not an exhaustive bibliography, but simply the list of works cited in this study.
Bakeman, Kenneth. "Stringing Techniques of Harpsichord Builders" in The Galpin Society Journal, Number XXVII, pp.95-112, May 1974.
Boalch, Donald H. Makers of the Harpsichord and Clavichord 1440-1840. 2nd Edition. Clarendon Press, Oxford (UK) 1974.
Boalch, Donald H. Makers of the Harpsichord and Clavichord 1440-1840. 3rd Edition. ed. Charles Mould. Oxford Univ. Press, Oxford (UK) 1995.
Bonza, Augusto. Musei e gallerie di Milano - Museo degli strumenti musicali - Catalogo - Strumenti a Tastiera. Electa, Milan 1997.
Brauchli, Bernard. "The 1782 Taskin Harpsichord, Colares, Portugal" in The Galpin Society Journal, Number LIII, pp.25-50, April 2000.
Corrette, Michel. Le Maitre du Clavecin pour l'Accompagnement, Méthode Theorique et Pratique. Paris 1753.
Di Veroli, Claudio. Unequal Temperaments: Theory, History and Practice (Scales, Tuning and Intonation in Musical Performance). 2nd revised edition, Bray Baroque, Bray, Ireland 2009. http://temper.braybaroque.ie/
Di Veroli, Claudio. Playing the Baroque Harpsichord: Essays on the Instrument, Interpretation and Performance, with relevant topics for the Clavichord and Organ. Bray Baroque, Bray (Ireland) 2010. http://play.braybaroque.ie
Donahue, Thomas. "A Method of Designing a Harpsichord String Plan" in Music and Its Questions: Essays in Honor of Peter Williams (ed. Thomas Donahue). OHS Press, Richmond VA (USA) 2007.
Donahue, Thomas. "Evaluating Historical Stringing Information" in Early Keyboard Journal Vol. 25/26 pp. 125-151. USA 2008.
Ellis, Alexander. Appendix XX, Sections H: "The History of Musical Pitch in Europe", contributed to Ellis's English translation of Helmholtz's On the Sensations of Tone (see Helmholtz 1862/1885).
Hubbard, Frank. Three Centuries of Harpsichord Making. Harvard University Press, Cambridge, Massachusetts (USA) 1965.
Irvin, Paul Y. "Historical Keyboard Instruments-the Vocal Ideal, and other Historical Questions" in Sounding Board No.3 Nov. 2010. British Harpsichord Society 2010. WWW. http://www.harpsichord.org.uk/soundingboard.php (quoted as "2010a")
Irvin, Paul Y. "Understanding Musical Wire" in Clavichord International. Bennebroek (Netherlands) 2010. (quoted as "2010b")
Helmholtz, Hermann L.F. Lehre von den Tonempfindungen… Heidelberg 1862. English edition: On the Sensations of Tone, Longmans, London 1885. (see Ellis)
Koster, John. Keyboard Musical Instruments in the Museum of Fine Arts, Boston. Museum of Fine Arts, Boston 1994.
Louchet, Jean. The Keyboard Stringing Guide. Châtillon (France), 2009.
O'Brien, Grant. "Some principles of eighteenth-century harpsichord stringing and their application" in The Organ Yearbook, 12 (1981) 160-76.
O'Brien, Grant. Information on stringing for the following entries: 4329-Jean Goermans/Pascal Taskin, Paris 1764-83 and 4315-Pascal Taskin, Paris 1769 (both from the Russell Collection). Edinburgh 2000. http://www.music.ed.ac.uk/euchmi/ucki.html
O'Brien, Grant. "Criteria for the Determination of Original Stringing … 1785 Longman and Broderip Harpsichord" in Aspects of Harpsichord Making in the British Isles (John Koster ed.). Pendragon, New York 2010.
Raymond Russell. The Harpsichord and Clavichord. Faber and Faber, London 1959, 2nd. Ed. rev. 1973.
Raymond Russell. Victoria and Albert Museum - Catalogue of Musical Instruments - Volume I: Keyboard Instruments. Her Majesty's Stationery Office, London 1968.
Victoria & Albert Museum. Harpsichord, Pascal-Joseph Taskin (I) and Charles Fleury (restorers), Paris, France, 1786 and 1856. London, undated webpage. http://www.vam.ac.uk/collections/furniture/furniture_features/musical_instruments/objects/object.php?action=next&id=44
Wraight, Denzil. "Principles and Practice in Stringing Italian Keyboard Instruments" in Early Keyboard Journal, Vol. 18, pp.175-238. Chapel Hill, NC (USA) 2000.
˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜˜
USE OF THIS TEXT, TERMS AND CONDITIONS
Quoting text: Copying text from this webpage and inserting it in other publications or webpages is automatically allowed provided the following conditions are met:
a) As customary, the text copied must be included between quotation marks and left unmodified except for deletions. The latter should not change the meaning in any way and should be identified with ellipses.
b) The source must be quoted as "TASKIN HARPSICHORD SCALINGS AND STRINGINGS REVISITED, Bray Baroque, Bray, Ireland 2011. http://harps.braybaroque.ie/Taskin_stringing.htm".
c) The author should be immediately notified by email: see http:/play.braybaroque.ie for details.
Quotes/copies not adhering to the conditions indicated above will be considered in violation of the author's copyright and legal action may follow.
Disclaimer: The assertions made here about persons and writings are based on evidence from duly acknowledged published material, current at February 2011. The author will not accept responsibility from any offence or damage caused by reading this webpage: its contents is read and used at the user's own risk. For any issues re the above, please feel free to email the author: see http:/play.braybaroque.ie for details.
Page last updated:
22-Mar-2016